All Hands on Deck

	Historical Background on USS Constitution USS Constitution is the oldest commissioned warship afloat in the world. Carrying a crew of 450 men and over 50 guns, she was launched in 1797 to protect America's freedom on the seas. She was undefeated against the British in the War of 1812 and earned the nickname "Old Ironsides" when a sailor saw a cannon ball bounce off her thick, wooden hull during battle. When she was declared unseaworthy in 1828, she was saved by the American people who rallied for her preservation. After a long career, including capturing a slave ship, circumventing the globe, and serving as a military prison, she is now berthed in Boston and is open to the public. For more information, go to www.allhandsondeck.org, www.ussconstitutionmuseum.org, and www.ussconstitution.navy.mil.

Objectives
After completing this lesson, students will be able to:

	1.	Write an equation for the vertical height and horizontal distance, or range, of a cannonball as it leaves Constitution.
	2.	Identify the maximum height of the cannonball algebraically and graphically.
	3.	Identify the amount of time it would take for the cannonball to reach an enemy vessel algebraically.
	4.	Determine if a cannonball would hit the intended target algebraically.

Massachusetts Math Curriculum Frameworks

	•	PC.P.3 Demonstrate an understanding of the trigonometric functions (sine, cosine, tangent, cosecant, secant, and cotangent). Relate the functions to their geometric definitions.
	•	PC.G.2 Use the notion of vectors to solve problems. Describe addition of vectors, multiplication of a vector by a scalar, and the dot product of two vectors, both symbolically and geometrically. Use vector methods to obtain geometric results. (12.G.3)
	•	PC.G.2 Use dimensional analysis for unit conversion and to confirm that expressions and equations make sense. (12.M.2)

Materials

	•	Worksheet (pdf): Firing the Cannons on Constitution
	•	Answer Key (pdf): Firing the Cannons on Constitution

Procedure

The difficult part of this lesson is the amount of prerequisite mathematical knowledge. Students must be familiar with right triangle trigonometry, vectors, and finally, the vertical motion mathematics from the first part of the lesson.

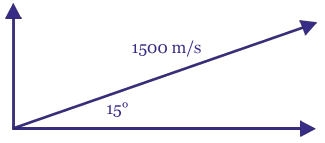
A vector is quantity in which both the magnitude and the direction are stated. For example, I could be driving at 35 mph, which is just speed. If I am driving north 35 mph, I now have velocity, which is also a vector.

Start with the 1500 m/s problem and move slowly through the beginning. The important aspects of the drawing are shown below.

The students' drawings may not include the horizontal and vertical arrows, but they are the most important attribute of the modeling of the situation. The slanted arrow is the velocity vector of the cannonball. The horizontal arrow represents the horizontal component of the velocity vector and the vertical arrow represents the vertical component of the velocity vector. In the previous lesson, we only used the vertical component.

Simply put, we graph on a horizontal/vertical coordinate system, so we need to convert the slanted vector into a horizontal and vertical component. This is where the right triangle trigonometry comes in handy. To calculate the vertical component of the velocity evaluate:
v_y = v₀ sin , where v₀ represent the initial velocity and represents the angle of inclination. Similarly, the horizontal component can be evaluated with v_x = v₀ cos .

Example:

v₀ = 1500 m/s and = 15⁰

v_y = v₀ sin = 1500 sin 15⁰ 388.2 m/s

v_x = v₀ cos = 1500 cos 15⁰ 1477 m/s

These values should make sense because the cannon is fired horizontally. The cannon is angled slightly vertically, so the vertical component of velocity is smaller in comparison.

The rest of the questions on the worksheet are solved similarly to those of the past lesson.

to top