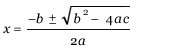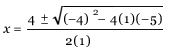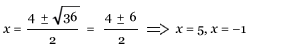All Hands on Deck

	Historical Background on USS Constitution USS Constitution is the oldest commissioned warship afloat in the world. Carrying a crew of 450 men and over 50 guns, she was launched in 1797 to protect America's freedom on the seas. She was undefeated against the British in the War of 1812 and earned the nickname "Old Ironsides" when a sailor saw a cannon ball bounce off her thick, wooden hull during battle. When she was declared unseaworthy in 1828, she was saved by the American people who rallied for her preservation. After a long career, including capturing a slave ship, circumventing the globe, and serving as a military prison, she is now berthed in Boston and is open to the public. For more information, go to www.allhandsondeck.org, www.ussconstitutionmuseum.org, and www.ussconstitution.navy.mil.

Objectives
After completing this lesson, students will be able to:

	1.	Write an equation for the vertical height of a cannonball as it leaves Constitution.
	2.	Identify the maximum height of the cannonball algebraically and graphically.
	3.	Identify the amount of time it would take for the cannonball to reach an enemy vessel algebraically.
	4.	Determine when a cannonball would hit the intended target algebraically.

Massachusetts Math Curriculum Frameworks

	•	AII.P.6 Given algebraic, numeric and/or graphical representations, recognize functions as polynomial, rational, logarithmic, or exponential. (12.P.6)
	•	AII.P.7 Find solutions to quadratic equations (with real coefficients and real or complex roots) and apply to the solutions of problems. (12.P.7)
	•	AII.P.8 Solve a variety of equations and inequalities using algebraic, graphical, and numerical methods, including the quadratic formula; use technology where appropriate. Include polynomial, exponential, and logarithmic functions; expressions involving the absolute values; and simple rational expressions. (12.P.8)
	•	AII.P.11 Solve everyday problems that can be modeled using polynomial, rational, exponential, logarithmic, and step functions, absolute values and square roots. Apply appropriate graphical, tabular, or symbolic methods to the solution. Include growth and decay; logistic growth; joint (e.g., I = Prt, y = k(w₁ + w₂)), and combined (F = G(m₁m₂/d²)) variation. (12.P.11)
	•	AII.P.12 Identify maximum and minimum values of functions in simple situations. Apply to the solution of problems. (12.P.12)

Materials

	Worksheets (pdf):
	•	A. Firing the Cannons on Constitution
	•	B. Solving with the Quadratic Formula
	•	C. Firing the Cannons on Constitution

Procedure

The mathematical object of this lesson is to analyze different qualities of quadratic polynomials, or polynomial equations with degree equal to 2, such as maximums, minimums and zeros. The common characteristic the graph of a quadratic, or parabola, is the U shape which may open up or down. All of the examples will open down.

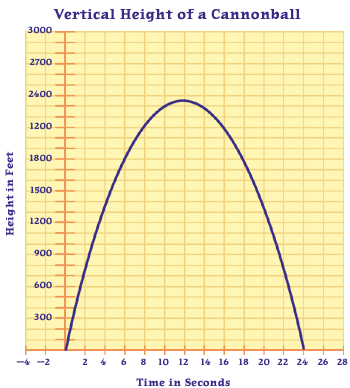
The vertical height of a cannonball can be modeled with the
projectile motion equation:
where the h(t) represents the vertical distance determined by time, g represents the acceleration due to gravity, v₀ represents the initial upward velocity and h₀ represents the initial height. The acceleration due to gravity is roughly either 32 feet/s² or 9.8 m/s².

Note: This method only gives vertical distance. Horizontal distance is not taken into account. In order to account for horizontal distance, we would need to use vectors and trigonometry. See the second part of this lesson for these methods.

Students will also need the aid of a calculator to evaluate the quadratic formula. All decimals may be rounded to the nearest tenth. Make sure that students use units in their final answers.

Begin with the worksheet showing the vertical height of a cannonball. Talk with the students about different aspects of the graph, such as symmetry, maximum height, and zeros, or x-intercepts.

Walk the students through writing an equation for the graph. The necessary information is given to the students so it becomes an exercise in identifying and substituting.

The equation for this example is: h(t) = –16t² + 388t + 24

Distribute worksheet A. Allow students the time to answer questions.

We eventually want to move to a pure algebraic way of solving these problems. The students need to be familiar with the quadratic formula, a formula that solves for the zeros, or x-intercepts of a quadratic equation.

Quadratic formula:

Note: The equation must be solved for zero to use the formula.

Example 1: Solve x² – 4x = 5

	Step 1: Solve for zero
		x² – 4x – 5 = 0

	Step 2: Identify a, b, and c
		a = 1, b = –4, and c = –5

	Step 3: Substitute the values into the formula


	Step 4: Evaluate

If the students need remediation, there are 4 examples on worksheet B (this can also be used for homework or practice).

The other algebraic value that we need to calculate is the maximum value. This point will be calculated by using the symmetric quality of the graph. All parabolas have a vertical axis of symmetry at , where a and b are the same coefficients as those used in the quadratic formula. Since this is the x value for the maximum point, plug x into the graph's equation, h(t), to solve for the height.

Example 2: Calculate the maximum height of the parabola h(t) = –16t ² + 388t + 24

	Step 1: Identify a, b, and c
		a = –16, b = 388

	Step 2: Substitute a and b into


	Step 3: Evaluate

The maximum height of the ball is achieved after 12.125 seconds. To find the height after 12.125 seconds, substitute the time into the original equation for height and evaluate.

h(12.125) = –16(12.125)² + 388(12.125) + 24 = –2352.25 + 4704.5 +24 = 2376.25 feet

It may be necessary to review these skills before moving any further.

When you feel satisfied with the skills, move onto worksheet C and the 24-pound cannonball problem. The students should be able to answer the first four questions without much assistance from the teacher, but they will need help with the last two. Both of these questions are applications of the quadratic formula.

to top